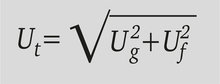Qu'est-ce qui détermine le flou géométrique dans les radiographies ?
1. Effets géométriques :
- Taille de la source
- Distance entre la source et l'objet
- Distance entre le défaut et le film
2. Propriétés du film (régissant la qualité de l'image) :
- Grain
- Contraste
- Voile
- Flou inhérent
3. Qualité du rayonnement appliqué.
Qu'est-ce qui détermine le flou géométrique dans les radiographies ?
Flou géométrique
Du fait des dimensions finies de la focale ou de la taille de la source, les tubes radiogènes et les sources radioactives produisent toujours une certaine quantité de flou, appelé « flou géométrique » (Ug dans la fig. 1-11), sur les radiographies.
L'ampleur de ce flou (Ug) est donné par l'équation suivante :
La formule suivante permet de calculer la valeur maximale de Ug liée à un défaut situé à une distance maximale du film (et pour lequel a = t) :
Dans ce cas, les images floues de chacun des deux bords du défaut peuvent se chevaucher (exemple C). Le résultat est que l'image C devient non seulement floue, mais qu'elle subit également une réduction du contraste par rapport à l'image A, réalisée avec une source ponctuelle, et à l'image B, réalisée avec une source relativement petite.
Flou inhérent
Non seulement les cristaux d'halogénures d'argent directement exposés au rayonnement X prennent la forme de grains d'argent, mais le volume qui environne l'émulsion aussi (à un degré moindre). Cette section transversale représente le « flou inhérent » ou « flou du film » Uf.
Ainsi, même en l'absence de flou géométrique, si l'énergie de rayonnement est assez élevée, le flou du film, dit « flou inhérent », peut apparaître. Lorsqu'une plaque d'essai en acier de forte transition d'épaisseur est radiographiée avec des rayons X à haute énergie, il y aura transition graduelle de la densité du film sur l'image de « l'étape » de A à B.
Sans flou inhérent, le film montrerait une transition tout à fait nette entre les deux densités (figure 3a-11). Dans la pratique, et comme le montre les figures 3b, 3c et 3d-11, la densité change sur l'image.
La largeur de cette zone de transition (Uf), exprimée en mm, est une mesure du flou du film.
Le tableau 1-11 et la figure 4-11 montrent les valeurs de flou inhérent déterminées expérimentalement pour un film exposé à différents niveaux d'énergie de rayonnement. Ces valeurs sont basées sur l'utilisation de filtres et d'écrans renforçateurs en plomb minces ; les écrans plus épais donnent des valeurs légèrement supérieures. En l'absence d'écrans renforçateurs, la valeur de Uf est 1,5 fois à 2 fois plus petite. Uf dépend principalement de l'intensité du rayonnement et du type d'écrans renforçateurs employé ; le type de film n'a quasiment aucun impact.
La distance entre le film et l'écran renforçateur a une importance capitale sur la valeur de Uf.
Il est impératif que le film et l'écran renforçateur soient bien en contact et, pour ce faire, il est possible de les emballer sous-vide.
À partir des informations ci-dessus, on peut constater que la valeur de Uf augmente avec des énergies de rayonnement supérieures.
Flou total
La combinaison de Ug et Uf permet de déterminer le flou total du film, Ut. Il ne suffit pas d'additionner les deux valeurs pour obtenir celle de Ut.
Dans la pratique, la meilleure approximation du flou total d'un film Ut est donnée par la formule suivante :
En gros, si l'une des valeurs de flou (Ug ou Uf ) fait plus de deux fois la valeur de l'autre, le flou total est égal à la valeur la plus importante ; si les deux valeurs de flou sont identiques, le flou total est environ égal à √2 = 1,4 fois la valeur unique.
Au besoin, il est possible de réduire la valeur de Ug en augmentant la distance entre le film et la focale. Cette possibilité est toutefois limitée car, du fait de la loi du carré inverse, les temps d'exposition seraient alors extrêmement longs. Choisir une distance optimale entre la focale et le film (F) où Ug = Uf est donc un compromis.
Il est par conséquent possible d'augmenter la distance entre le film et l'objectif pour réduire la valeur de Ug. Toutefois, compte tenu de la loi du carré inverse, cette augmentation de distance a des limites, car les temps d'exposition seraient extrêmement longs. La formule indique également que le flou géométrique prend de plus en plus d'importance à mesure qu'augmente la distance entre le défaut et le film.
L'utilisation d'un tube radiogène à micro-focalisation dont la taille de focale est comprise entre 10 et 50 µm est cependant un cas particulier. Avec une taille de focale aussi petite, il est possible d'agrandir délibérément l'image en utilisant une courte distance entre la source et l'échantillon et une grande distance entre l'échantillon et le film, tout en conservant une petite valeur de Ug acceptable.
L'avantage de cette technique, appelée « procédé de grossissement projectif », est que le grain toujours présent dans une image photographique perturbe moins la perceptibilité des très petits défauts.
La Figure 2-11 montre l'effet du flou géométrique sur l'image d'un défaut de taille inférieure à celle de la focale.