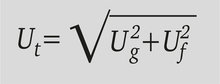决定射线照相几何不清晰度的因素有哪些？

1. 几何效应：

• 放射源大小
• 放射源到物体的距离
• 缺陷到胶片的距离

2. 胶片特性（影响图像质量）：

• 颗粒度
• 对比度
• 雾度
• 固有不清晰度

3. 辐射质量。

决定射线照相几何不清晰度的因素有哪些？

几何不清晰度

由于焦点或放射源尺寸有限，X 射线管和放射源生成的射线照片始终会有一定程度的模糊，即“几何不清晰度”，图 1-11 中的 U_g。

这种不清晰度的大小，即 U_g，以下列公式表示：

Image

根据公式可以计算出与位于距胶片最远处（a = t）的缺陷有关的 Ug 的最大值：

Image

在这种情况下，如示例 C 所示，缺陷两侧边缘的非清晰图像可能会重叠。 其结果是，与使用点放射源拍摄的图像 A 和使用相对较小放射源拍摄的图像 B 相比，图像 C 不仅变得不清晰，而且对比度也会降低。

固有不清晰度

不仅直接暴露在 X 射线下的卤化银晶体会形成银粒，乳剂的周围也会形成银粒（尽管程度较轻）。 这个横截面积就是“固有不清晰度”或“胶片不清晰度”U_f。

因此，即使没有几何不清晰度，如果辐射能量足够高，也会产生胶片不清晰度：即所谓的“固有不清晰度”。 如果用高能 X 射线对厚度急剧变化的测试钢制板进行射线照相，则在整个“阶跃”（从 A 到 B）图像中会呈现出胶片密度的逐渐变化。

如图 3a-11 所示，如果没有固有不清晰度，胶片会在两种密度之间呈现出完全清晰的过渡。 实际上，整个图像中的密度变化如图 3b、3c 和 3d-11 所示。

过渡区域的宽度 (U_f) 以毫米为单位，是胶片不清晰度的测量值。

表 1-11 和图 4-11 展示了曝光在不同能量等级的辐射下时胶片固有不清晰度的实验测定值。 这些数值是在使用滤光片和薄铅增感屏的基础上得出的；较厚的增感屏得出的数值会略高。 如果不使用铅屏，则 U_f 会小 1.5 到 2 倍。 U_f 主要受辐射强度和所用增感屏类型的影响；胶片类型几乎没有影响。

胶片与增感屏之间的距离对 U_f 值会产生很大影响。

胶片与增感屏之间需要保持良好的接触，这可以通过将胶片和增感屏真空包装在一起来实现。

Image

从以上信息可以推断出，辐射能量越高，U_f 值越大。 

总体不清晰度

胶片的总体不清晰度 Ut 由 U_g 和 U_f 共同决定。 不能仅仅通过将这两个值简单相加来得出 U_t 的值。

实际上，以下公式可以得出胶片不清晰度 U_t 的最佳近似值：

Ut Formula

大体上，如果一个不清晰度值（U_g 或 U_f）是另一个值的两倍以上，则总体不清晰度等于最大的单个值；如果两个不清晰度值相等，则总体不清晰度约为单个值的 √2 = 1.4 倍。

必要时，可以通过增大焦点到底片的距离来降低 U_g。 但这只能在有限的范围内实现，因为根据平方反比定律，曝光时间会变得非常长。 作为折中方案，我们选择了一个最合适的焦点到底片距离 F，其中 U_g = U_f。