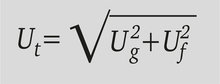¿Qué elementos determinan la borrosidad geométrica en las radiografías?
1. Efectos geométricos:
- Tamaño de la fuente
- Distancia fuente-objeto
- Distancia entre el defecto y la película
2. Propiedades de la película (que rigen la calidad de la imagen):
- Granulosidad
- Contraste
- Niebla
- Borrosidad inherente
3. Calidad de la radiación aplicada.
¿Qué elementos determinan la borrosidad geométrica en las radiografías?
Borrosidad geométrica
Los tubos de rayos X y las fuentes radiactivas siempre producen radiografías con cierta borrosidad: la «borrosidad geométrica», Ug en la fig. 1-11, debido a las dimensiones finitas del punto focal o el tamaño de la fuente.
La magnitud de esta borrosidad, Ug, viene dada por la siguiente ecuación:
El valor máximo de Ug relacionado con un defecto situado a una distancia máxima de la película (y para el cual a = t) se puede calcular a partir de la fórmula:
En esta situación, las imágenes borrosas de cada uno de los dos bordes del defecto pueden superponerse, como se muestra en el ejemplo C. El resultado es que la imagen C no solo pierde nitidez, sino que también sufre una reducción de contraste en comparación con la imagen A, hecha con una fuente puntual y la imagen B hecha con una fuente relativamente pequeña.
Borrosidad inherente
No solo los cristales de haluro de plata expuestos directamente a la radiación X se forman en granos de plata, sino también (aunque en menor grado) el volumen de emulsión circundante. Esta área de sección transversal representa la «borrosidad inherente» o «borrosidad de la película» Uf.
Por lo tanto, incluso en ausencia de borrosidad geométrica, si la energía de radiación es lo suficientemente alta, puede ocurrir una borrosidad en la película: la llamada «borrosidad inherente». Si se radiografía una placa de prueba de acero con una transición brusca de espesor con rayos X de alta energía, habrá una transición gradual de la densidad de la película a lo largo de la imagen del «escalón» de A a B.
Sin la borrosidad inherente, la película mostraría una transición absolutamente nítida entre las dos densidades, como se muestra en la figura 3a-11. En la práctica, el cambio de densidad en la imagen es como se muestra en las figuras 3b, 3c y 3d-11.
La anchura de esta zona de transición (Uf), expresada en mm, es una medida de la borrosidad de la película.
La tabla 1-11 y la figura 4-11 muestran valores determinados experimentalmente de borrosidad inherente para películas expuestas a varios niveles de energía de radiación. Estos valores se basan en el uso de filtros y pantallas intensificadoras de plomo fino; las pantallas más gruesas producen valores ligeramente más altos. Si no se utilizan pantallas de plomo, Uf es de 1,5 a 2 veces menor. Uf depende principalmente de la intensidad de la radiación y el tipo de pantallas intensificadoras utilizadas; el tipo de película apenas influye.
La distancia entre la película y la pantalla intensificadora es de gran importancia para el valor de Uf.
Es imperativo un buen contacto entre la película y la pantalla intensificadora y se puede lograr envasando al vacío la película y las pantallas juntas.
De la información anterior se puede deducir que Uf aumenta con energías de radiación más altas.
Borrosidad total
La borrosidad total de la película Ut está determinada por la combinación de Ug y Uf. Los dos valores no se pueden simplemente sumar para llegar a una cifra para Ut.
En la práctica, la siguiente fórmula produce la mejor aproximación para la borrosidad de la película Ut:
En términos generales, si un valor de borrosidad (Ug o Uf) es más del doble del valor del otro, la borrosidad total es igual al valor individual más grande; Si ambos valores de borrosidad son iguales, la borrosidad total es aproximadamente √2 = 1,4 veces el valor único.
Si es necesario, Ug se puede reducir aumentando la distancia entre el enfoque y la película. Esto solo se puede hacer de forma limitada porque, debido a la ley del cuadrado inverso, los tiempos de exposición serían extremadamente largos. Como compromiso se elige una distancia F óptima entre el foco y la película, donde Ug = Uf.
En consecuencia, Ug se puede reducir a cualquier valor requerido aumentando la distancia entre la fuente y la película. Sin embargo, dada la ley del cuadrado inverso, esta distancia no se puede aumentar ilimitadamente, ya que se producirían tiempos de exposición extremadamente largos. La fórmula también indica que la borrosidad geométrica adquiere cada vez más importancia a medida que aumenta la distancia entre el defecto y la película.
Sin embargo, surge un caso especial cuando se utiliza un tubo de rayos X de microenfoque con un tamaño de punto focal en el rango de 10 a 50 µm. Con un tamaño de enfoque tan pequeño, la imagen se puede ampliar deliberadamente utilizando una distancia corta entre la fuente y la muestra y una distancia grande entre la muestra y la película, y aun así conservar un valor aceptablemente pequeño de Ug.
La ventaja de esta técnica, denominada «método de ampliación proyectiva», es que la granulosidad siempre presente en una imagen fotográfica es un factor menos perturbador en la discernibilidad de defectos muy pequeños.
La Figura 2-11 muestra el efecto de la borrosidad geométrica en la imagen de un defecto más pequeño que el tamaño del enfoque.