Utilisation d'une courbe (densité) caractéristique avec un graphique d'exposition

Comment utiliser la courbe caractéristique (densité) avec un graphique d'exposition ?

Dans les exemples suivants, la tension du tube et la distance entre la focale et le film (DFD) sont supposées constantes, et le développement automatique prend 8 minutes dans le révélateur G135 à 28°C.

Effet de l'épaisseur de l'objet sur la densité de l'image radiographique

Un objet en acier comprenant deux sections d'épaisseur différente de 12 et 15 mm doit être radiographié sur film D7. Le graphique d'exposition de la figure 7-9 montre qu'à 160 kV avec une distance DFD de 70 cm et une exposition de 10 mA.min, on obtient une densité de 2 derrière la section mesurant 15 mm d'épaisseur.

Question : Quelle sera la densité d'image derrière la section de 12 mm dans ces conditions ?

Méthode et réponse

Le graphique d'exposition (fig. 7-9) montre que, dans les conditions indiquées ci-dessus, la densité D = 2 sur le film D7 à travers la section de 15 mm d'épaisseur, en utilisant une exposition de 10 mA.min (point A sur le graphique).

Dans les mêmes conditions, la section de 12 mm nécessiterait une exposition de 5 mA.min (point B du graphique), c'est-à-dire un rapport d'exposition de 10/5. L'exposition à travers la section de 12 mm est deux fois plus grande que celle de la section de 15 mm. Le logarithme de ce ratio est égal à 0,3 (log 2 = 0,3).

La courbe caractéristique (fig. 8-9) du film D7 montre qu'une densité de 2 correspond à l'exposition relative logarithmique 2,2 (point C sur la fig. 8-9). À 12 mm, l'exposition relative logarithmique est égale à 2,2 + 0,3 = 2,5. La densité correspondante est alors de 3,5 (point D sur la fig. 8-9).

Effet de l'exposition sur le contraste

Supposons qu'avec une exposition de 15 mA.min pour une radiographie sur film D7, la densité moyenne et le contraste s'avèrent trop faibles après traitement. La densité la plus élevée et la plus faible dans la section la plus pertinente de l'image sont seulement de 1,5 et 0,5. L'objectif était d'effectuer une radiographie avec une densité maximale de 3,0.

Questions : quel temps d'exposition serait nécessaire pour la même intensité de rayonnement et quelle serait l'augmentation du contraste ?

Méthode et réponse

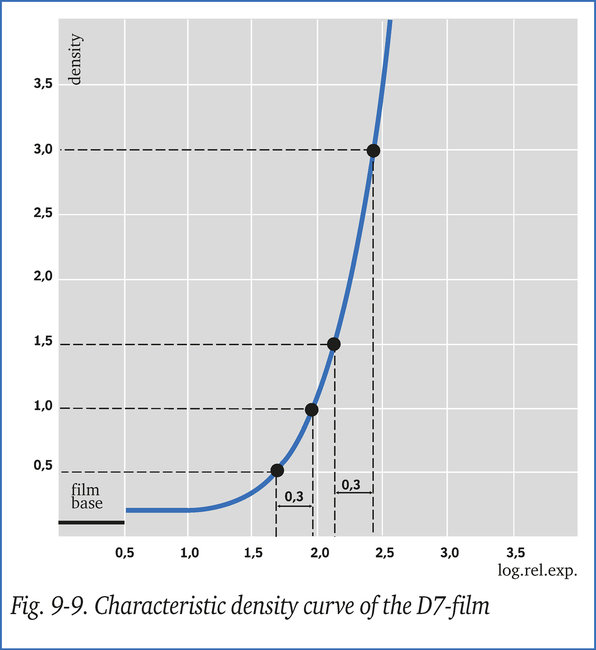
La courbe caractéristique (fig. 9-9) montre qu'aux densités mesurées (respectivement 1,5 et 0,5), le logarithme correspondant des expositions relatives est de 2,15 et 1,65.

La densité de 3,0 ne devant pas être dépassée, la zone la plus importante pour l'interprétation, d'une densité de 1,5 sur la première exposition, doit maintenant indiquer 3,0. La courbe caractéristique (fig. 9-9) montre que la densité de 3,0 correspond à une exposition relative logarithmique de 2,45 et que la différence entre les deux valeurs est égale à 2,45 - 2,15 = 0,3.

Cela signifie que le temps d'exposition doit être doublé (100,3 = 2), ce qui donne une dose de rayonnement de 30 mA.min. Cela répond à la première question.

Si l'on double le temps d'exposition, l'exposition relative logarithmique de la valeur de densité la plus faible initialement mesurée augmentera de 0,3, c.-à-d. 1,65 + 0,3 = 1,95. La densité correspondante sera alors de 1,0 (fig. 9-9).

Sur la radiographie d'origine, le gradient moyen entre les densités supérieure et inférieure était de (1,5 - 0,5) / (2,15 - 1,65) = 2,0. Le gradient moyen de la nouvelle radiographie étant égal à (3,0 - 1,0) / (2,45 - 1,95) = 4,0, le contraste moyen a doublé.