Uso da curva característica (densidade) com gráfico de exposição

Como utilizo a curva característica (densidade) com um gráfico de exposição?

Nos exemplos a seguir, a tensão do tubo e a distância foco-filme (FFD) são consideradas constantes, e a revelação automática ocorre durante 8 minutos no revelador G135 a 28 °C.

Efeito da espessura do objeto na densidade da imagem radiográfica

É necessário radiografar, em filme D7, um objeto de aço composto por duas seções de espessuras diferentes de 12 mm e 15 mm. O gráfico de exposição da figura 7-9 mostra isso em 160 kV e um FFD de 70 cm, utilizando 10mA.min, obteremos uma densidade de 2 atrás da seção medindo 15 mm de espessura.

Pergunta: que densidade de imagem será obtida atrás da seção medindo 12 mm nessas condições?

Método e resposta

O gráfico de exposição (fig.7-9) mostra que nas condições mencionadas acima a densidade D = 2 é obtida no filme D7 por meio da seção de 15 mm de espessura, utilizando uma exposição de 10 mA.min, ponto A do gráfico.

Nas mesmas condições, a seção de 12 mm exigiria uma exposição de 5 mA.min (ponto B no gráfico), o que significa uma relação de exposição de 10/5. A exposição pela seção de 12 mm é duas vezes maior do que pela seção de 15 mm. O logaritmo desta relação é igual a: 0,3 (log 2 = 0,3).

A curva característica (fig. 8-9) do filme D7 mostra que a densidade 2 corresponde ao log da exposição relativa 2,2 (ponto C na fig. 8-9). Aos 12 mm o log. da exposição rel. é 2,2 + 0,3 = 2,5. A densidade correspondente é então 3,5 (ponto D na fig. 8-9).

Efeito da exposição no contraste

Suponha que quando uma exposição de 15 mA.min é usada para uma radiografia em filme D7, tanto a densidade média quanto o contraste se mostram muito baixos após o processamento. A densidade mais alta e mais baixa na seção mais relevante da imagem são apenas 1,5 e 0,5. A intenção era fazer uma radiografia com densidade máxima de 3,0.

Perguntas: Qual tempo de exposição seria necessário para a mesma intensidade de radiação e que aumento de contraste seria alcançado?

Método e resposta

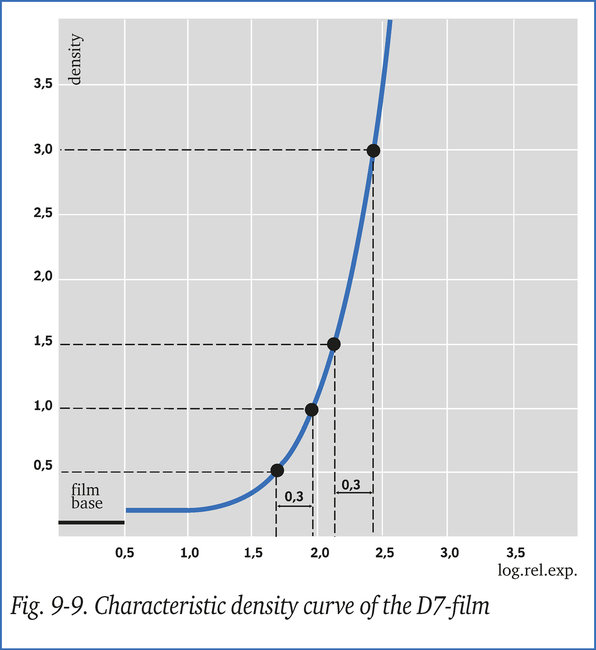
A curva característica (fig. 9-9) mostra que nas densidades medidas de 1,5 e 0,5 respectivamente, o logaritmo correspondente das exposições relativas é 2,15 e 1,65.

Como a densidade 3,0 não deve ser excedida, a área mais importante para a interpretação, que apresentou densidade 1,5 na primeira exposição, deve agora exibir 3,0. A curva característica, figura 9-9, mostra que a densidade 3,0 corresponde ao log. da exp. rel. 2,45 e a diferença entre os dois valores é 2,45 - 2,15 = 0,3.

Isso significa que o tempo de exposição deve ser duplicado (100,3 = 2), resultando em uma dose de radiação de 30 mA.min. Isso responde à primeira pergunta.

Se o tempo de exposição for duplicado, o log. da exposição rel. do valor de densidade mais baixo originalmente medido aumentará em 0,3, ou seja, 1,65 + 0,3 = 1,95. A densidade correspondente será 1,0 (fig. 9-9).

O gradiente médio entre as densidades superior e inferior na radiografia original foi de (1,5 - 0,5) / (2,15 - 1,65) = 2,0. O gradiente médio na nova radiografia é (3,0 - 1,0) / (2,45 - 1,95) = 4,0, portanto o contraste médio dobrou.