Verwendung der Schwärzungskurve (Dichtekurve)mit einem Belichtungsdiagramm
Wie verwende ich die Schwärzungskurve (Dichtekurve) mit einem Belichtungsdiagramm?
In den folgenden Beispielen werden die Röhrenspannung und der Fokus-Film-Abstand (FFA) als konstant angenommen und die automatische Entwicklung erfolgt 8 Minuten lang bei 28 °C im Entwickler G135.
Einfluss der Dicke eines Objekts auf die Dichte des Röntgenbildes
Es soll ein Stahlobjekt mit zwei Abschnitten unterschiedlicher Dicke von 12 mm und 15 mm auf D7 Film durchstrahlt werden. Im Belichtungsdiagramm in Abbildung 7-9 ist erkennbar, dass bei 160 kV und einem FFA von 70 cm bei 10 mA.min eine Dichte von 2 hinter dem 15 mm dicken Abschnitt erreicht wird.
Frage: Welche Bildqualität wird hinter dem 12 mm dicken Abschnitt unter den vorgegebenen Bedingungen erreicht?
Methode und Antwort
Das Belichtungsdiagramm (Abb.7-9) zeigt, dass unter den oben genannten Bedingungen auf D7-Film Dichte D = 2 über den15 mm dicken Abschnitt, mit einer Belichtung von 10 mA.min erreicht wird, Punkt A im Diagramm.
Unter denselben Bedingungen würde der 12 mm dicke Abschnitt eine Belichtung von 5 mA.min (Punkt B im Diagramm) erfordern, was einem Belichtungsverhältnis von 10/5 entspricht. Die Belichtung durch den 12 mm dicken Abschnitt ist zweimal größer als durch den 15 mm dicken Abschnitt. Der Logarithmus dieses Verhältnisses ist: 0,3 (log 2 = 0,3).
Die Schwärzungskurve (Abb. 8-9) des D7 Films zeigt, dass die Dichte 2 der log. relativen Belichtung 2,2 entspricht (Punkt C in Abb. 8-9). Bei 12 mm beträgt die log. rel. Belichtung 2,2 + 0,3 = 2,5. Die zugehörige Dichte beträgt dann 3,5 (Punkt D in Abb. 8-9).
Einfluss der Belichtung auf den Kontrast
Ausgehend von einer Belichtung von 15 mA.min für ein Röntgenbild auf D7 Film erweisen sich sowohl die durchschnittliche Dichte als auch der Kontrast nach dem Entwickeln als zu gering. Die höchste und niedrigste Dichte im relevantesten Abschnitt des Bildes sind nur 1,5 und 0,5. Das Ziel war es, ein Röntgenbild mit einer maximalen Dichte von 3,0 zu erstellen.
Fragen: Welche Belichtungszeit wäre für dieselbe Strahlungsintensität erforderlich und welche Kontraststeigerung würde erreicht werden?
Methode und Antwort
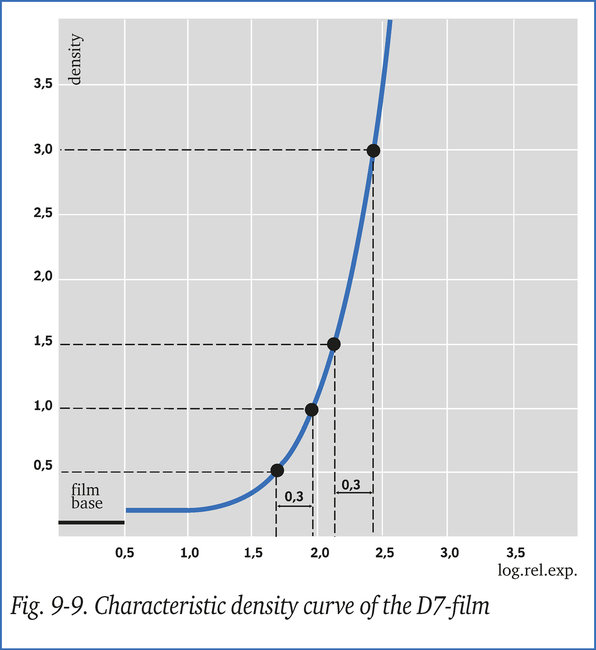
Die Schwärzungskurve (Abb. 9-9) zeigt, dass bei den gemessenen Dichten von 1,5 und 0,5 der entsprechende Logarithmus der relativen Belichtungen 2,15 und 1,65 ist.
Da die Dichte von 3,0 nicht überschritten werden sollte, muss der für die Interpretation wichtigste Bereich, der bei der ersten Belichtung eine Dichte von 1,5 hatte, jetzt 3,0 aufweisen. Die Schwärzungskurve in Abbildung 9-9 zeigt, dass die Dichte von 3,0 einer log. rel. Belichtung von 2,45 entspricht und die Differenz zwischen den beiden Werten 2,45 - 2,15 = 0,3 beträgt.
Das bedeutet, dass die Belichtungszeit verdoppelt werden muss (100,3 = 2), was zu einer Strahlendosis von 30 mA.min führt. Damit ist die erste Frage beantwortet.
Wird die Belichtungszeit verdoppelt, steigt die log. rel. Belichtung des ursprünglich gemessenen niedrigsten Dichtewerts um 0,3, d. h. 1,65 + 0,3 = 1,95. Die entsprechende Dichte beträgt 1,0 (Abb. 9-9).
Die durchschnittliche Steigung zwischen den oberen und den unteren Dichten beim ursprünglichen Röntgenbild betrug (1,5 - 0,5) / (2,15 - 1,65) = 2,0. Die durchschnittliche Steigung beim neuen Röntgenbild beträgt (3,0 - 1,0) / (2,45 - 1,95) = 4,0; somit hat sich der durchschnittliche Kontrast verdoppelt.