Uso de la curva característica (densidad) con un diagrama de exposición
¿Cómo puedo usar la curva característica (densidad) con un diagrama de exposición?
En los siguientes ejemplos, se supone que la tensión del tubo y la distancia entre el foco y la película (FFD) son constantes y que el revelado automático dura 8 minutos en un revelador G135 a 28 °C.
Efecto del grosor del objeto sobre la densidad de la imagen radiográfica.
Se requiere radiografiar, en película D7, un objeto de acero que comprende dos secciones de diferente grosor de 12 mm y 15 mm. El diagrama de exposición, figura 7-9, muestra que a 160 kV y con una FFD de 70 cm, utilizando 10 mA.min, se obtendrá una densidad de 2 detrás de la sección de 15 mm de grosor.
Pregunta: ¿Qué densidad de imagen se obtendrá detrás de la sección de 12 mm en estas condiciones dadas?
Método y respuesta
En el diagrama de exposición (fig. 7-9) se muestra que bajo las condiciones mencionadas anteriormente se obtiene una densidad D = 2 en la película D7 a través de la sección de 15 mm de grosor, usando una exposición de 10 mA.min, punto A en el diagrama.
En las mismas condiciones, la sección de 12 mm requeriría una exposición de 5 mA.min (punto B del diagrama), lo que supone una relación de exposición de 10/5. La exposición a través de la sección de 12 mm es dos veces mayor que a través de la sección de 15 mm. El logaritmo de esta relación es igual a: 0,3 (log 2 = 0,3).
La curva característica (fig. 8-9) de la película D7 muestra que la densidad 2 corresponde a la exposición relativa logarítmica 2,2 (punto C en la fig. 8-9). A 12 mm, la exposición relativa logarítmica es 2,2 + 0,3 = 2,5. La densidad correspondiente es entonces de 3,5 (punto D en la fig. 8-9).
Efecto de la exposición sobre el contraste
Supongamos que cuando se utiliza una exposición de 15 mA.min para una radiografía en película D7, tanto la densidad media como el contraste resultan ser demasiado bajos después del procesamiento. La densidad más alta y más baja en la sección más relevante de la imagen son solo de 1,5 y 0,5. La intención era realizar una radiografía con una densidad máxima de 3,0.
Preguntas: ¿Qué tiempo de exposición se necesitaría para la misma intensidad de radiación y qué aumento de contraste se lograría?
Método y respuesta
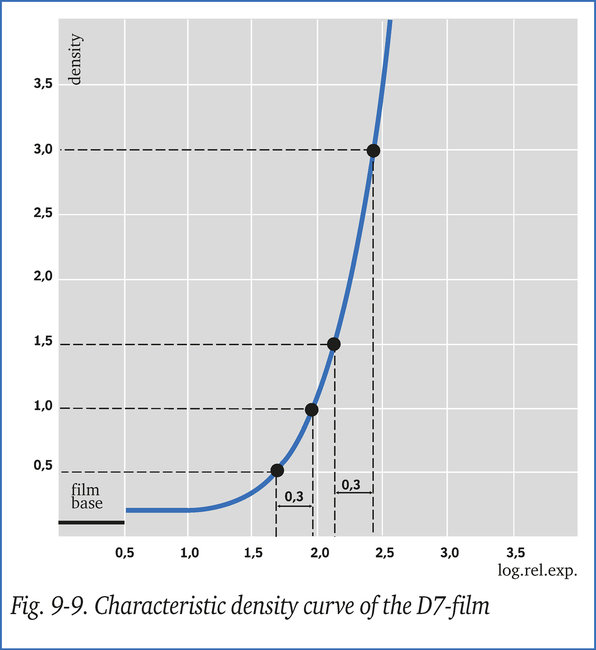
La curva característica (fig. 9-9) muestra que con densidades medidas de 1,5 y 0,5 respectivamente, el logaritmo correspondiente de las exposiciones relativas es 2,15 y 1,65.
Dado que no se debe exceder la densidad de 3,0, el área más importante para la interpretación, que mostró una densidad de 1,5 en la primera exposición, ahora debe mostrar 3,0. La curva característica, figura 9-9, muestra que la densidad de 3,0 corresponde con la exposición relativa logarítmica de 2,45 y la diferencia entre ambos valores asciende a 2,45 - 2,15 = 0,3.
Esto significa que se debe duplicar el tiempo de exposición (100,3 = 2), lo que da como resultado una dosis de radiación de 30 mA.min. Esto responde a la primera pregunta.
Si se duplica el tiempo de exposición, la exposición rel. log. del valor de densidad más bajo medido originalmente aumentará en 0,3, es decir, 1,65 + 0,3 = 1,95. La densidad correspondiente será de 1,0 (fig. 9-9).
El gradiente promedio entre las densidades superior e inferior en la radiografía original fue (1,5 - 0,5)/(2,15 - 1,65) = 2,0. El gradiente promedio en la nueva radiografía es (3,0 - 1,0) / (2,45 - 1,95) = 4,0, por lo que el contraste promedio se ha duplicado.