Uso della curva caratteristica (di densità) con un grafico delle esposizioni

Come posso usare la curva caratteristica (di densità) con un grafico delle esposizioni?

Negli esempi seguenti la tensione del tubo e la distanza messa a fuoco-pellicola (FFD) sono considerate costanti e lo sviluppo automatico è di 8 minuti nel rivelatore G135 a 28 °C.

Effetto dello spessore dell'oggetto sulla densità dell'immagine radiografica

Per la radiografia su pellicola D7 è necessario un oggetto in acciaio che abbia due sezioni di spessori diversi, di 12 mm e 15 mm. Il grafico delle esposizioni in figura 7-9 mostra che, a 160 kV e a una FFD di 70 cm, utilizzando 10 mA.min si otterrà una densità di 2 dietro la sezione con lo spessore di 15 mm.

Domanda: Quale densità dell'immagine si otterrà dietro la sezione da 12 mm in queste date condizioni?

Metodo e risposta

Il grafico delle esposizioni (fig. 7-9) mostra che, alle condizioni indicate in precedenza, la densità D = 2 si ottiene per le pellicole D7 attraverso la sezione di 15 mm di spessore, utilizzando un'esposizione di 10 mA.min, punto A sul grafico.

Alle stesse condizioni, la sezione da 12 mm richiederà un'esposizione di 5 mA. min (punto B nel grafico), il che significa un rapporto di esposizione di 10/5. L'esposizione attraverso la sezione da 12 mm è due volte maggiore rispetto a quella attraverso la sezione da 15 mm. Il logaritmo di questo rapporto è uguale a: 0,3 (log 2 = 0,3).

La curva caratteristica (fig. 8-9) della pellicola D7, mostra che la densità 2 corrisponde all'esposizione relativa logaritmica 2,2 (punto C nella fig. 8-9). A 12 mm, l'esposizione rel. log. è 2,2 + 0,3 = 2,5. La densità corrispondente è quindi 3,5 (punto D in fig. 8-9).

Effetto dell'esposizione sul contrasto

Presumiamo che, quando viene utilizzata un'esposizione di 15 mA. min per una radiografia su una pellicola D7, sia la densità media che il contrasto dimostrino di essere troppo bassi dopo l'elaborazione. La densità più alta e quella più bassa nella sezione più rilevante dell'immagine sono solo 1,5 e 0,5. L'intenzione era effettuare una radiografia con una densità massima di 3,0.

Domande: Quale tempo di esposizione sarebbe necessario per la stessa intensità di radiazioni e quale incremento di contrasto si otterrebbe?

Metodo e risposta

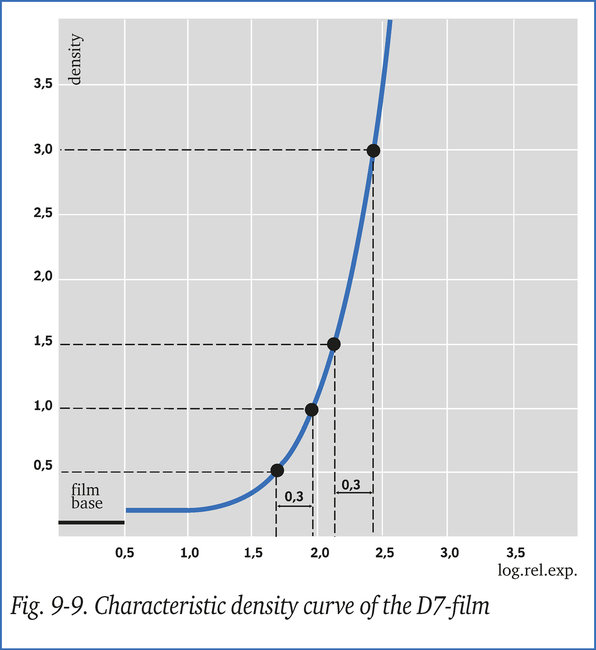
La curva caratteristica (fig. 9-9) mostra che, alle densità misurate di 1,5 e 0,5 rispettivamente, i logaritmi corrispondenti delle esposizioni relative sono 2,15 e 1,65.

Poiché la densità 3,0 non deve essere superata, l'area più importante ai fini dell'interpretazione, che mostrava la densità 1,5 sulla prima esposizione, deve ora visualizzare 3,0. La curva caratteristica, figura 9-9, mostra che la densità di 3,0 corrisponde all'esp. rel. log. di 2,45 e la differenza tra i due valori ammonta a 2,45 - 2,15 = 0,3.

Ciò significa che il tempo di esposizione deve essere raddoppiato (100,3 = 2), comportando una dose di radiazioni di 30 mA.min. Questa è la risposta alla prima domanda.

Se il tempo di esposizione viene raddoppiato, l'esposizione rel. log. del valore di densità inferiore originalmente misurato aumenterà di 0,3, ovvero 1,65 + 0,3 = 1,95. La densità corrispondente sarà 1,0 (fig. 9-9).

Il gradiente medio tra le densità superiore e inferiore sulla radiografia originale sarà (1,5 - 0,5)/(2,15 - 1,65) = 2,0. Il gradiente medio sulla nuova radiografia è (3,0 - 1,0)/(2,45 - 1,95) = 4,0, pertanto il contrasto medio è raddoppiato.